Conformal Prediction as Bayesian Quadrature

Jake C. Snell
Princeton University
Thomas L. Griffiths
Princeton University
ICML 2025
ICML Outstanding Paper

Paper Code arXiv Reviews Poster

Overview

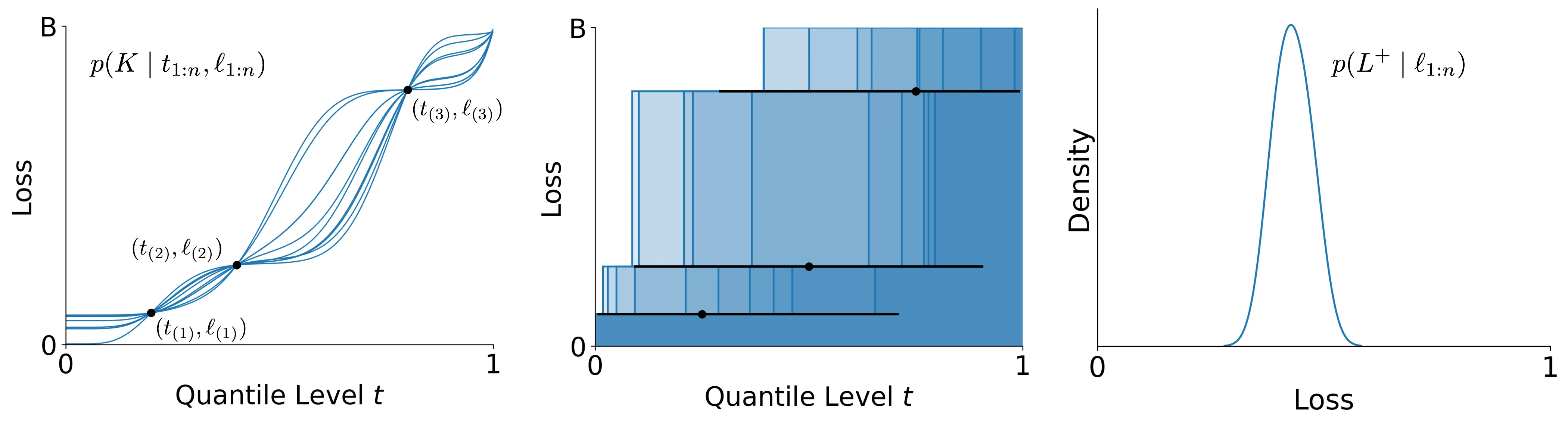
In this work, we revisit the foundations of conformal prediction and discover exciting new connections to Bayesian quadrature.

Contributions:

1.) We reformulate conformal prediction as prior-agnostic Bayesian quadrature.

2.) We show how to recover conformal prediction from the posterior mean estimate.

3.) Our distributional view controls risk better with just a small modification to vanilla conformal prediction.

Our Approach

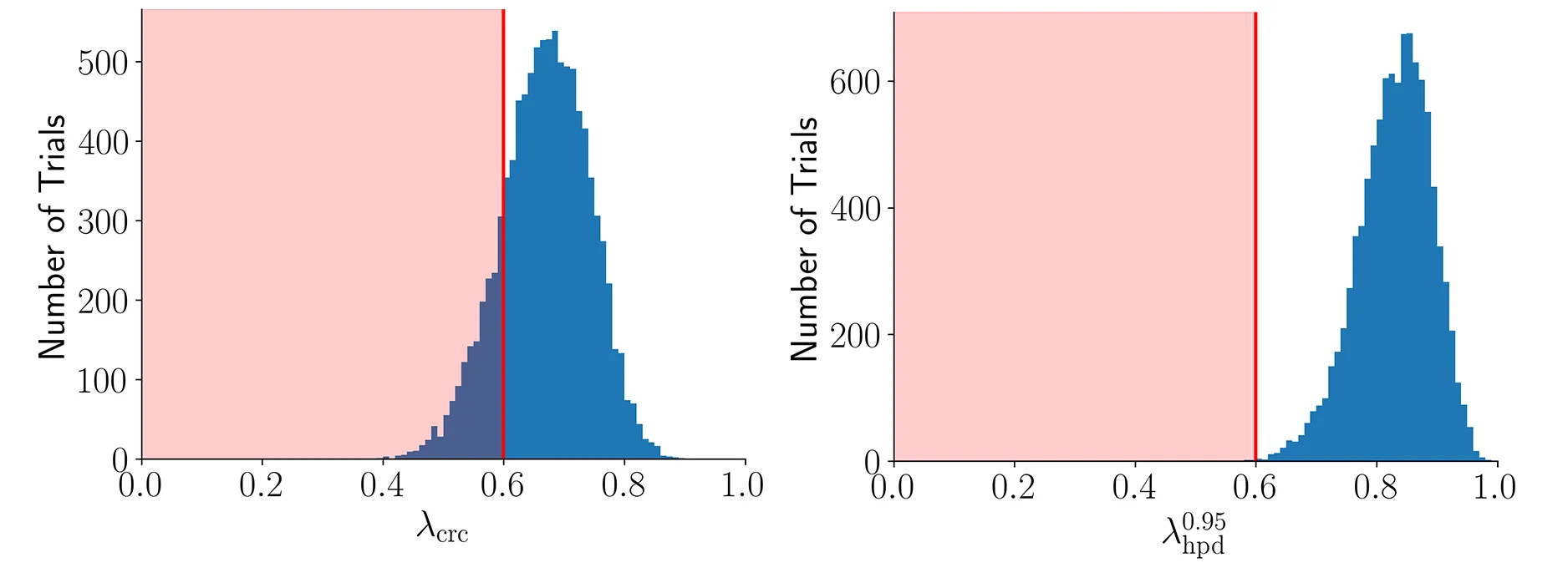
Overview of our approach.
Figure 1. A conventional Bayesian quadrature approach to conformal prediction (left) would place a prior over the quantile function of the loss distribution. Our approach (middle) combines properties of quantile spacings with a right rectangular integration rule to construct an upper bound (right) on the posterior distribution of the expected loss.

Results

Overview of our approach.
Figure 2. Conformal prediction and conformal risk control (left) provide coverage/risk guarantees with probability over the calibration data. Our approach (right) enables more precise control over the risk by selecting λ\lambda such that the highest posterior density (HPD) interval for the risk, conditioned on the observed calibration data, is contained within the acceptable risk region.
Table 1. Results controlling false negative rate of multilabel classification on MS-COCO. Our approach more closely targets the desired maximum failure rate of 5% while maintaining small prediction sets.
MethodFailure Rate95% Confidence IntervalPrediction Set Size
Conformal Risk Control45.0%[44.1%, 46.0%]2.9
Risk-controlling Prediction Sets0.0%[0.00%, 0.04%]3.6
Ours (β=0.95\beta = 0.95)5.4%[5.0%, 5.9%]3.0

Citation

    @inproceedings{
    snell2025conformal,
    title={Conformal Prediction as Bayesian Quadrature},
    author={Jake C. Snell and Thomas L. Griffiths},
    booktitle={Forty-second International Conference on Machine Learning},
    year={2025},
    url={https://openreview.net/forum?id=PNmkjIzHB7}
}